Hexo
0%

6-最小生成树MST

发表于

最小生成树MST

一个有 n 个结点的连通图的生成树是原图的极小连通子图，且包含原图中的所有 n 个结点，并且有保持图连通的最少的边。

(1)MST性质

  1. 无环
  2. 连接所有节点
  3. N个节点，N-1条边
  4. 权值和：树上所有边的权值的总和
  5. 最小生成树MST满足权值和最小，即最小生成树其实是最小权重生成树的简称
  6. 当各边有相同权值时，由于选择任意性最小生成树不唯一；
    当各边权值不同时，最小生成树是唯一的

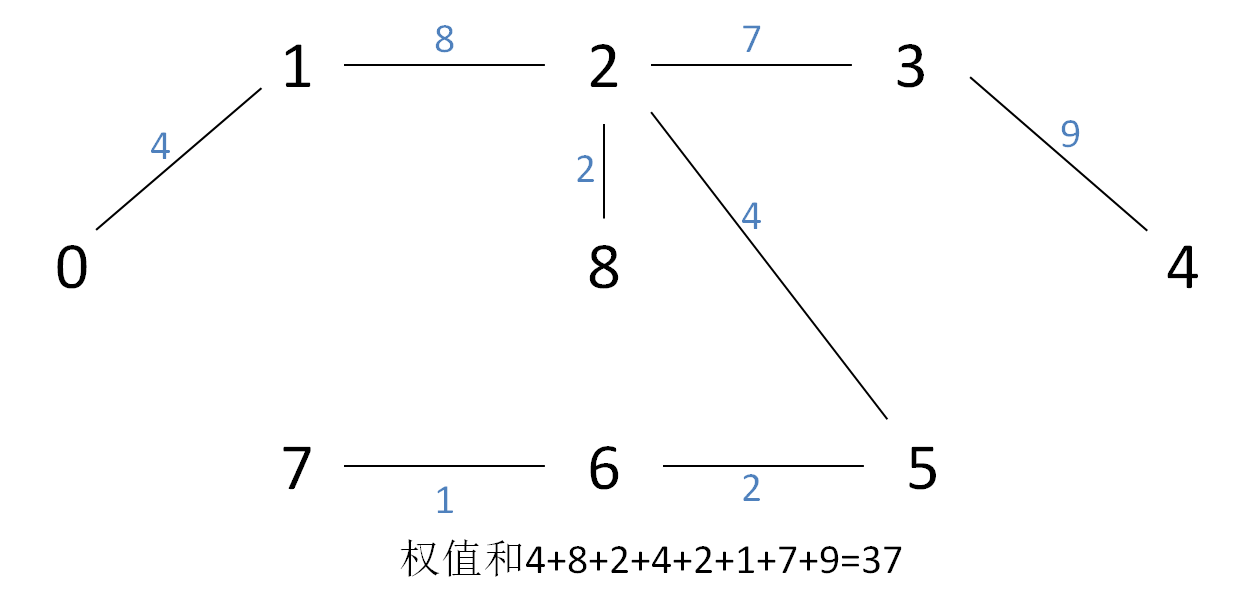
eg:给出一个例子图

img1

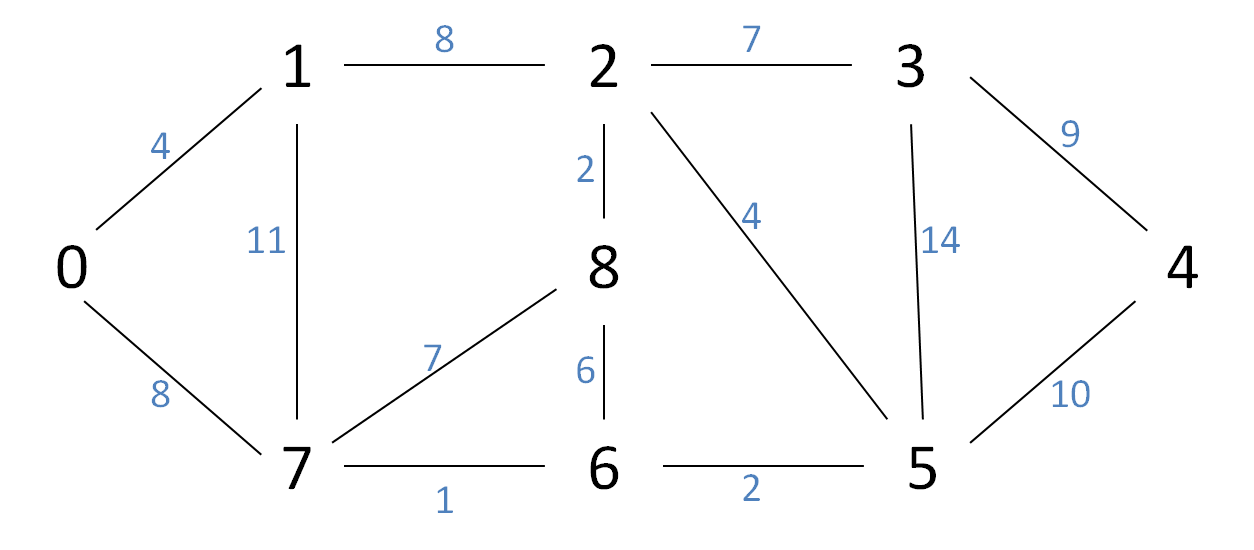
(2)常用方法：

  1. 克鲁斯卡尔Kruskal：直接选择权值最小的边
  2. 普利姆Prim：从顶点除法，间接选择权值较小的边

(3)克鲁斯卡尔Kruskal

  1. 将所有边取出，并按权值升序排序
  2. 每次取出当前权值最小的边回帖到图中，判断是否出现环（并查集），若无环，则该边是最小生成树的一条边，若有环，则丢弃该边

eg:给出例子图的克鲁斯卡尔方法的MST

img2

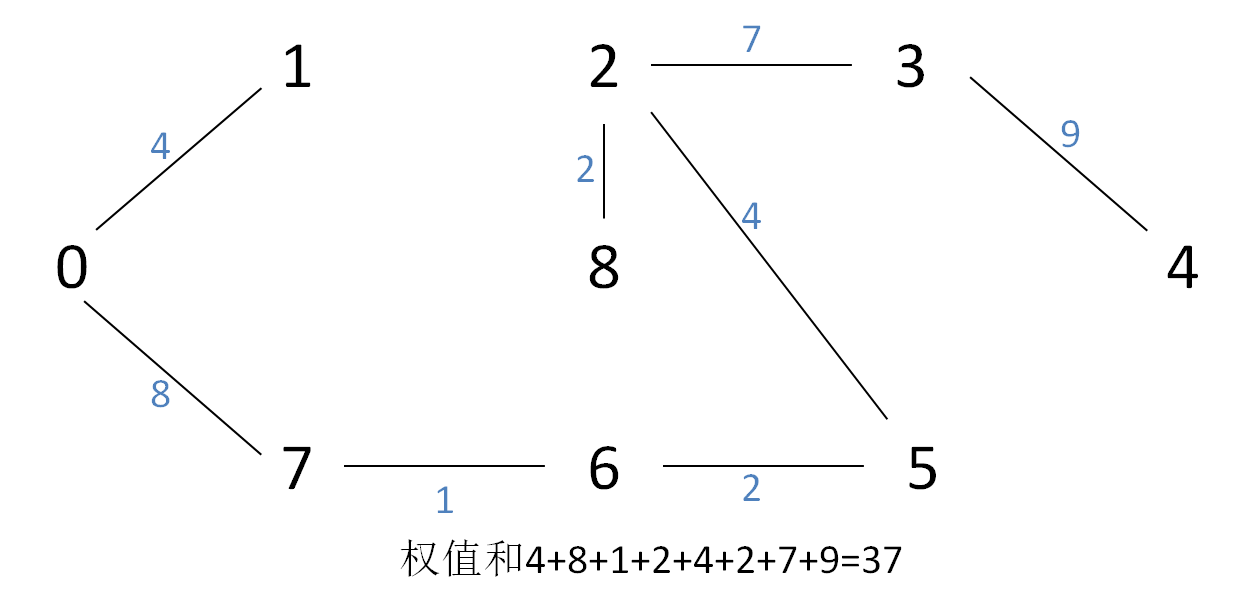
(4)普利姆Prim

  1. 确定起始点
  2. 数组1：selected标记每个顶点是否已经被选择
    数组2：minDust处理每个未选节点到已选节点集合的最小距离
    数组3：parent记录已选取边的父节点是谁，指最小生成树的父节点
  3. 选取minDust中最小的边加入到已选节点集合中，更新三个数组

eg:给出例子图的普利姆方法的MST

img3