树状数组BIT
设计目标:给定一个长度为n的数组,实现两个功能
(1)lowbit
求非负整数x在二进制下最低位的11
2
3
4int lowbit(int x)
{
return x&(-x);
}
(2)树状数组
给出一个长度为n=8的数组a,并给出树状数组t的可视化图形,t[i]所对应的a[start]~a[end]的区间和
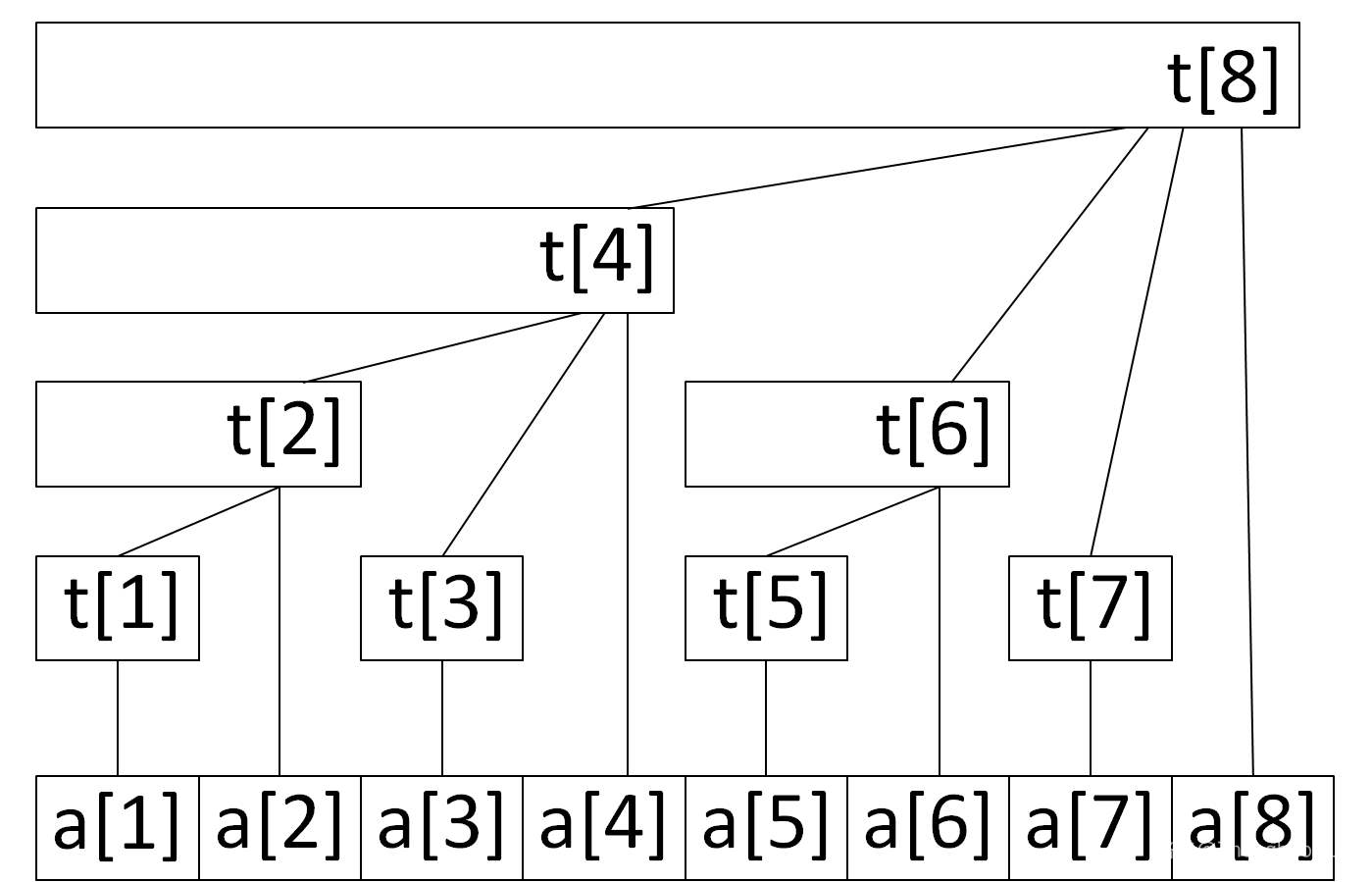
- 所有下标以1开始,且t[0]=0
- 树状数组t[x]保存以x为根的子树中叶节点值的和
- 将t[x]中x转换为二进制后,每层末尾0个数相同,且0的个数与覆盖长度有关。
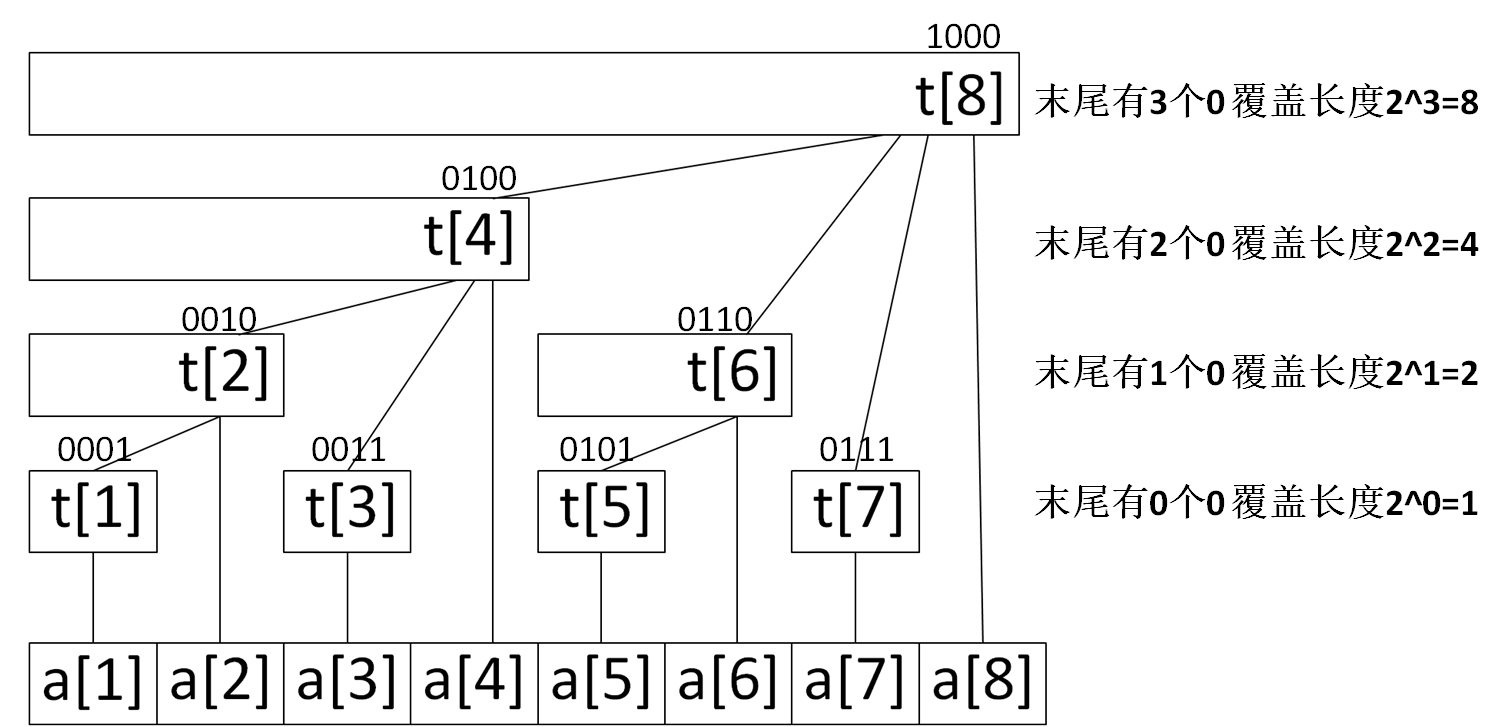
- t[x]节点的覆盖长度等于
lowbit(x) - t[x]节点的父节点是
t[x+lowbit(x)] - 整棵树的深度为log2(n)+1,n为数组长度即叶子节点个数
(3)add(x,k)单点自增
让a[x]+=k;
注意不是修改成k,而是自增k1
2
3
4
5void add(int x,int k)
{
for (;x<=n;x+=lowbit(x))
t[x]+=k;
}
(4)ask(x)包括开头的区间查询
查询a[1]~a[x]的区间和1
2
3
4
5
6
7int ask(int x)
{
int ans=0;
for (;x>0;x-=lowbit(x))
ans+=t[x];
return ans;
}
(5)interval_sum(x,y)区间和查询
查询a[x]~a[y]的区间和,可以借助ask(x)来间接操作1
2
3
4int interval_sum(int x,int y)
{
return ask(y)-ask(x-1);
}